Phần bài tập về dao động điều hòa là phần không thể thiếu trong đề thi THPT Quốc gia. Trong bài viết này tôi sẽ tổng hợp lại cho các bạn một số các dạng bài tập về dao động điều hòa thường gặp và cách giải quyết chúng.
Dạng 1: Viết phương trình trong dao động điều hòa
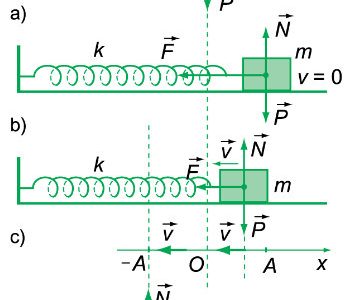
· Phương trình li độ dao động điều hòa:
x = Acos(ωt+ φ).
· Phương trình vận tốc:
v = x’(t) = – ωA sin(ωt+φ) = ωA cos(ωt+φ+π2 )
· Phương trình gia tốc:
a = -ω2Acos(ωt+ φ) = ω2Acos(ωt+ φ+ π) = -ω2x
BÀI TẬP:
Câu 1: Trong các phương trình sau phương trình nào không biểu thị cho dao động điều hòa?
A. x = 5cosπt(cm).
B. x = 3sin(100πt + π/6)(cm).
C. x = 2sin2(2πt + π/6)(cm).
D. x = 3sin5πt + 3cos5πt(cm).
Câu 2: Vật dao động trên quỹ đạo dài 2cm, khi pha của dao động là π/6 vật có vận tốc v = 2π cm/s. Chọn gốc thời gian lúc vật có li độ cực đại. Phương trình dao động của vật là:
A. x = 2sin(4πt + π/2)(cm).
B. x = sin(4πt +π/2)(cm).
C. x = 2sin(πt – π/2)(cm).
D. x = sin(4πt – π/2)(cm).
Câu 3: Vật dao động điều hoà thực hiện 10 dao động trong 5s, khi vật qua vị trí cân bằng nó có vận tốc 62,8cm/s. Chọn gốc thời gian lúc vật qua vị trí có li độ x = 2,5√3 cm và đang chuyển động về vị trí cân bằng. Phương trình dao động của vật là
A. x = 5sin(4πt + 2π/3)(cm).
B. x = 20sin(πt +/3)(cm).
C. x = 5sin(4πt + π/3)(cm).
D. x = 20sin(2πt + 2π/3)(cm).
Dạng 2: Tính khoảng thời gian và đường đi trong dao động điều hòa
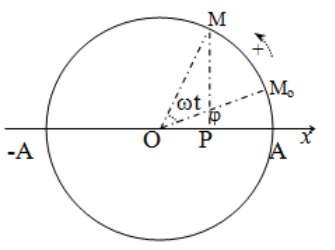
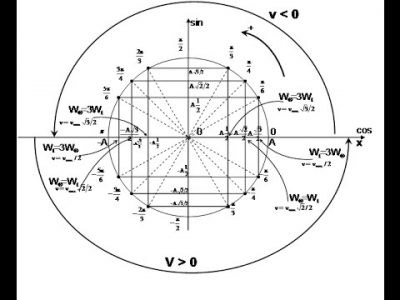
– Cách 1: Tính khoảng thời gian ngắn nhất để vật đi từ vị trí x1 đến vị trí x2: Sử dụng mối liên hệ giữa dao động điều hòa và chuyển động tròn đều
– Cách 2: Dùng công thức tính nhanh và máy tính cầm tay
o Khi vật đi từ VTCB đến li độ x hoặc ngược lại:
o Khi vật đi từ vị trí biên đến li độ x hoặc ngược lại:
BÀI TẬP:
Câu 1: Một vật dao động điều hoà với biên độ A = 6cm và chu kỳ T = 0,6s. Khoảng thời gian ngắn nhất là vật đi từ vị trí có li độ 3cm đến có li độ
A. 0,125s B. 0,175 s C. 0,15s D. 0,2s
Câu 2: Một chất điểm dao động điều hòa với biên độ 10 (cm) và tần số góc 10 (rad/s). Khoảng thời gian ngắn nhất để nó đi từ vị trí có li độ +3,5 cm đến vị trí cân bằng là
A. 0,036 s B. 0,121 s C. 2,049 s D. 6,951 s
Dạng 3: Tính quãng đường đi được trong thời gian t
– Biểu diễn t dưới dạng: t =nT + Dt; Trong đó n là số dao động nguyên, Dt là khoảng thời gian còn lẻ ra ( Dt < T ).
– Tổng quãng đường vật đi được trong thời gian t: S = n. 4A + Ds
Trong đó Ds là quãng đường vật đi được trong khoảng thời gian Dt, ta tính nó bằng cách sử dụng mối liên hệ giữa dao động điều hòa và chuyển động tròn đều.
BÀI TẬP:
Câu 1: Một vật nhỏ dao động điều hòa với biên độ A và chu kì T. Quãng đường đi được trong nT là: (n là số tự nhiên khác 0)
A. 3nA B. nA C. 2nA D. 4nA
Câu 2: Một vật dao động điều hòa theo phương trình Quãng đường vật đi được trong 5,5s
A. 93 cm B. 105 cm C. 154 cm D. 140 cm
Câu 3: Một vật dao động điều hòa với phương trình Quãng đường mà vật đi được trong thời gian 3s
A. 48 cm B. 15 cm C. 56 cm D. 32 cm
Dạng 4: Xác định trạng thái dao động của vật sau hoặc trước thời điểm t một khoảng
Kiểm tra xem nhận giá trị nào:
– Nếu thì và
– Nếu thì và
– Nếu có giá trị khác, ta dùng mối liên hệ dao động điều hòa và chuyển động tròn đều để giải tiếp:
o Bước 1: Vẽ đường tròn có bán kính R = A (biên độ) và trục Ox nằm ngang.
o Bước 2: Biểu diễn trạng thái của vật tại thời điểm t trên quỹ đạo và vị trí tương ứng của M trên đường tròn.
o Bước 3: Từ góc mà OM quét trong thời gian hạ hình chiếu xuống trục Ox suy ra vị trí, vận tốc, gia tốc của vật tại thời điểm t + hoặc t –
BÀI TẬP:
Câu 1: Một vật dao động điều hòa có phương trình: x = 2cos(2πt – π/6) (cm, s) Li độ và vận tốc của vật lúc t = 0,25s là:
A. 1cm ; ±2√3π.(cm/s). B. 1,5cm ; ±π√3(cm/s).
C. 0,5cm ; ±√3cm/s. D. 1cm ; ± π cm/s.
Câu 2: Một vật dao động điều hòa với phương trình: x = 4cos(20πt + π/6) cm. Chọn kết quả đúng:
A. lúc t = 0, li độ của vật là -2cm.
B. lúc t = 1/20(s), li độ của vật là 2cm.
C. lúc t = 0, vận tốc của vật là 80cm/s.
D. lúc t = 1/20(s), vận tốc của vật là – 125,6cm/s.
Dạng 5: Tính tốc độ trung bình và vận tốc trung bình
· Tốc độ trung bình: với S là quãng đường vật đi được trong khoảng thời gian .
=> Tốc độ trung bình trong 1 hoặc n chu kì là:
· Vận tốc trung bình: với là độ dời vật thực hiện được trong khoảng thời gian .
Độ dời trong 1 hoặc n chu kỳ bằng 0 => Vận tốc trung bình trong 1 hoặc n chu kỳ bằng 0.
BÀI TẬP:
Câu 1: Một vật dao động điều hòa với phương trình x = 6cos(20πt + π/6)cm. Vận tốc trung bình của vật đi từ vị trí cân bằng đến vị trí có li độ x = 3cm là:
A. 0,36m/s B. 3,6m/s C. 36cm/s D. Khác
Câu 2: Một vật dao động điều hòa theo phương trình x = 2cos(2πt + π/4) cm. Tốc độ trung bình của vật trong khoảng thời gian từ t = 2s đến t = 4,875s là:
A. 7,45m/s B. 8,14cm/s C. 7,16cm/s D. 7,86cm/s
Câu 3: Một chất điểm dao động điều hòa dọc theo trục Ox có vận tốc bằng không tại hai thời điểm liên tiếp (gần nhau nhất) là t1 = 1,75s; t2 = 2,5s; tốc độ trung bình trong khoảng thời gian đó là 16 cm/s. Ở thời điểm t = 0 chất điểm ở cách gốc tọa độ một khoảng là:
A. 2cm B. 4 cm C. 3cm D. 1cm
Dạng 6: Tìm số lần vật đi qua vị trí đã biết x (Hoặc v, a, Wt, Wđ, F) từ thời điểm đến
Trong mỗi chu kỳ, vật qua mỗi vị trí biên 1 lần còn các vị trí khác 2 lần (chưa xét chiều chuyển động) nên:
· Bước 1: Tại thời điểm , xác định điểm ; tại thời điểm , xác định điểm
· Bước 2: Vẽ đúng chiều chuyển động của vật từ tới , suy ra số lần vật đi qua là a.
ü Nếu < T thì a sẽ là kết quả, nếu >T thì số lần vật qua là 2n + a.
ü Nếu trùng với vị trí xuất phát thì số lần vật qua là 2n + a + 1.
BÀI TẬP:
Câu 1: Cho vật dao động điều hòa theo phương trình Số lần vật qua vị trí x = -5 cm trong 2,25s đầu tiên là:
A. 4 B. 5 C. 6 D. 7
Câu 2: Một chất điểm dao động điều hòa theo phương trình Trong một giây đầu tiên từ thời điểm t = 0, chất điểm đi qua vị trí có li độ x = 1cm bao nhiêu lần?
A. 7 lần B. 5 lần C. 4 lần D. 6 lần
Dạng 7: Tính thời điểm vật đi qua vị trí đã biết x (Hoặc v, a, Wt, Wđ, F) lần thứ n
· Bước 1: Xác định vị trí Mo tương ứng của vật trên đường tròn tại thời điểm
t = 0 và số lần vật qua vị trí x đề bài yêu cầu trong 1 chu kỳ ( thường là 1, 2 hoặc 4 lần).
· Bước 2: Thời điểm cần tìm là: , với:
ü n là số nguyên lần chu kỳ được xác định bằng phép chia hết giữa số lần gần số lần đề bài yêu cầu với số lần đi qua x trong 1 chu kỳ => Lúc này vật quay về vị trí ban đầu Mo, và còn thiếu số lần 1, 2… mới đủ số lần đề bài cho.
ü là thời gian tương ứng với góc quét mà bán kính OMo quét từ Mo đến các vị trí , ,… còn lại để đủ số lần.
BÀI TẬP:
Câu 1: Một vật dao động điều hòa với phương trình . Thời điểm vật qua vị trí x = 3cm lần thứ 5 kể từ lúc vật bắt đầu dao động là
A. 25/24 s
B. 1/8 s
C. 3/8 s
D. 1/12 s
Câu 2: Một vật dao động điều hòa với phương trình . Thời điểm đầu tiên vật qua vị trí x = 3cm theo chiều dương kể từ lúc vật bắt đầu dao động là
A. 1/8 s
B. 1/12 s
C. 1/24 s
D. 3/8 s
Câu 3: Một vật dao động điều hòa với phương trình . Thời điểm thứ 2014 vật qua vị trí có v = – cm/s là:
A. 1005,5 s
B. 2012 s
C. 1006,5 s
D. 1005 s
Xem thêm:
Lý thuyết + bài tập các dạng: Phương trình dao động điều hòa
Lý thuyết và bài tập về công thức độc lập thời gian vật lý 12